Linterna de Popa 373
Jorge Baca Campodónico
Diciembre de 2022
¿Se puede utilizar la ingeniería de control para disminuir la inflación?
¿Qué regla debe utilizar el BCRP para fijar su tasa de interés referencial?
Esta semana el BCRP volvió a elevar su tasa de interés referencial en 0.25 puntos porcentuales para ubicarla en 7.5%. Esta es la decimoséptima alza consecutiva que el BCRP realiza, en su afán de retornar la inflación del nivel actual de 8.5%, a la meta de inflación de 2 a 3%. Las primeras 13 alzas mensuales fueron de 0.50 puntos cada una, mientras que las últimas 4 han sido de solo 0.25 puntos porcentuales.
El BCRP tiene a su disposición una serie de herramientas para controlar indirectamente la inflación, siendo la tasa de interés de referencia la mas importante de ellas. El presidente del BCRP, Julio Velarde, en reciente entrevista a un medio periodístico argentino ha declarado, “…. La verdad es que la demanda de dinero es difícil de prever y por eso hoy casi ni veo los agregados monetarios. Nos manejamos con la tasa de interés…”.
¿Cuáles herramientas utiliza el BCRP? El BCRP viene utilizando una versión muy simple de controlador que se conoce como “regla de Taylor”, que es un controlador proporcional y que en forma esquemática se presenta en el Diagrama 1.
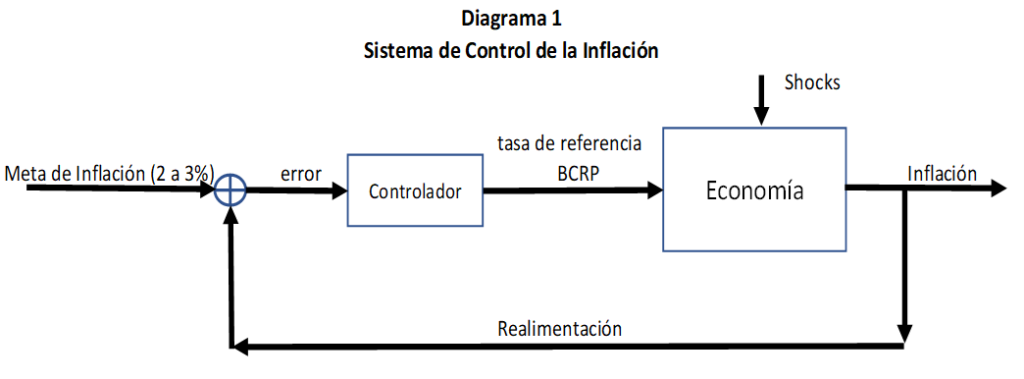
De acuerdo con la regla de Taylor, si la inflación observada (o en algunos modelos, la expectativa de inflación) se encuentra por encima (por debajo) de la meta de inflación entonces se genera una señal que gatilla el aumento (disminución) de la tasa de referencia del BCRP. Un aumento (disminución) de la tasa de referencia hace que la inflación de la economía caiga (aumente) y neutralice el impacto de los shocks como aumentos del precio del petróleo o desabastecimiento de algún producto.
El propósito de tener reglas como la regla de Taylor, introducida a partir de 1993, era tener una política monetaria simple y transparente que evitara crear shocks monetarios inesperados por parte de los bancos centrales para reducir las posibilidades de recesión, inflación y/o hiperinflación. La adopción de la regla de Taylor y las políticas de “metas de inflación” consagraron el concepto de que era preferible aplicar reglas que arriesgarse a una política monetaria caótica, ya sea que el caos fuera causado por discreción de las autoridades de los bancos centrales o eventos exógenos impredecibles como shocks de precios del oro o petróleo.
¿Por qué entonces el BCRP no está logrando reducir la inflación en los plazos anunciados? Si bien las reglas simples basadas en la regla de Taylor han venido funcionando relativamente bien por muchos años, desde fines de la década de 1990, se han venido desarrollando nuevas metodologías basadas en modelos macroeconómicos dinámicos, estocásticos y estimados empíricamente, incorporando el concepto de expectativas racionales.
Estos modelos se utilizaron para encontrar nuevas reglas de política, más complejas que la regla de Taylor, y para verificar la solidez de las nuevas reglas propuestas. La experiencia práctica de estos nuevos modelos coincidió con la reducción de la inflación mundial, al generalizarse la adopción de políticas monetarias basadas en “metas de inflación”.
A partir de la crisis del 2008 algunos bancos centrales comenzaron a aplicar la teoría del control óptimo, utilizando los nuevos modelos, refinados con fundamentos de microeconomía específicos, los llamados Modelos de Equilibrio General Dinámico Estocástico. El resultado fueron reglas complejas para los instrumentos de política que tenían la apariencia de “ajuste fino”, a diferencia de las simples reglas de política como la regla de Taylor.
La idea de que una política monetaria óptima llevada a cabo sin las limitaciones de reglas simples podría funcionar mejor que las reglas simples surgió en el contexto de los modelos macroeconómicos modernos. Estudios recientes utilizan el control óptimo para calcular la trayectoria más adecuada para la tasa de interés de referencia y la contrasta con los resultados obtenidos con reglas de política simples. Uno de los resultados de estos estudios afirma que una política agresiva de ajustes de la tasa de referencia da mejores resultados que la regla de Taylor.
En el caso peruano, una regresión econométrica que se muestra en la Tabla 1, demuestra, a manera de ejemplo, que la simple incorporación de un término adicional a la regla de Taylor mejora significativamente el impacto de la tasa de referencia sobre el control de la inflación.
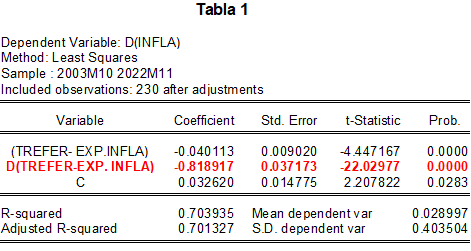
En este caso, la primera variable utilizada en la estimación del modelo es la diferencia entre la tasa de referencia y la expectativa de inflación (que es una variable comúnmente usada) y la variable adicional corresponde a la velocidad de cambio de esa primera variable (la primera derivada). La elevada significancia estadística (-22.03) de esa variable adicional nos dice que la velocidad de ajuste de la tasa de referencia es muy relevante en el control de la inflación.
¿Está el BCRP utilizando la mejor estrategia para contener la inflación? En términos de ingeniería de control, los resultados de la regresión nos indican que el controlador proporcional (que es la regla de Taylor) no es suficiente para controlar la inflación rápidamente y que la simple introducción de una variable adicional como, por ejemplo, la velocidad de cambio de la diferencia entre la tasa de referencia y la expectativa de inflación daría mejores resultados. Lamentablemente el BCRP continúa aplicando una metodología muy simple en el manejo de su política monetaria. (El contenido de esta columna se puede consultar en http://www.prediceperu.com/).
Excelente explicacion del concepto Taylor. me hace acordar que en automatizacion industrial se usa mucho ese modelo para controlar procesos, ya sea nivel, calor, flujo.https://es.wikipedia.org/wiki/Controlador_PID
habia uno de esos 3 creo que era el derivativo, el encargado de acelerar o retrazar la velocidad para que el proceso se estabilice. llevando esto al plano economico que Ud. explica, los aumentos del BCRP son muy insuficientes y deberian ser mas bruscos para forzar la inflacion hacia abajo.
muchas gracias por los comentarios
Excelente explicacion del concepto Taylor. me hace acordar que en automatizacion industrial se usa mucho ese modelo para controlar procesos, ya sea nivel, calor, flujo. es.wikipedia.org/wiki/Controlador_PID
habia uno de esos 3 creo que era el derivativo, el encargado de acelerar o retrazar la velocidad para que el proceso se estabilice. llevando esto al plano economico que Ud. explica, los aumentos del BCRP son muy insuficientes y deberian ser mas bruscos para forzar la inflacion hacia abajo.
muchas gracias por los comentarios